怎样求曲边梯形的面积?分几个步骤完成?每个步骤是什么?
求曲边梯形的面积的基本思路是:把曲边梯形分割成n个小曲边梯形→用小矩形近似替代小曲边梯形→求各小矩形的面积之和→求各小矩形面积之和的极限。
曲边梯形的底面积公式
梯形的面积公式是:上底加下底乘以高除以2梯形是上下两条边平行的四边形状,你按照一个对角线可以把它分成两个高相同的三角形,三角形面积公式是底乘以高除以2,所以梯形就是:上底乘以高除以2+下底乘以高除以2=上底。
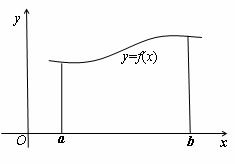
请问这类曲边梯形如何用微元法求面积
故,曲边梯形面积=∫(下c上d)[φ(y)-ψ(y)]dy
如何用定积分计算曲边梯形的面积?
=xe^(x^2)-1/2e^(x^2)+c =(x-1/2)e^(x^2)+c 对于一个给定的正实值函数,在一个实数区间上的定积分可以理解为在坐标平面上,由曲线、直线以及轴围成的曲边梯形的面积值(一种确定的实数值)。
以抛物线为曲边的,曲边梯形的面积怎么推导
1、函数求导 2、设抛物线的方程为 y=ax2+bx+c ,确定抛物线图上三个点的坐标,代入方程确定a、b、c的值,则可得出抛物线方程,将得到的抛物线方程求导,就可以得到曲边梯形的面积表达式,接着求出抛物线在x轴的两个。
