复合函数的定义域是怎么确定的
复合函数的定义域由内层函数和外层函数共同确定的。
已知y=f(x),u=g(x)。
则f(g(x))称为由f(x)和g(x)复合而成的复合函数,其中f(x)称外层函数,g(x)称内层函数。
若已知f(x)的定义域为(a,b),求f(g(x)。
复合函数定义域是什么?
复合函数的定义域由内层函数和外层函数共同确定的。
(1)f(x)的定义域,这就要求g(x)的值域在f(x)的定义域内,这时可以解得一个范围,在这个范围内g(x)的值域恰好是f(x)的定义域。
(2)g(x)本身的定义域,由于。
复合函数的定义域是什么
复合函数的定义域由内层函数和外层函数共同确定的。
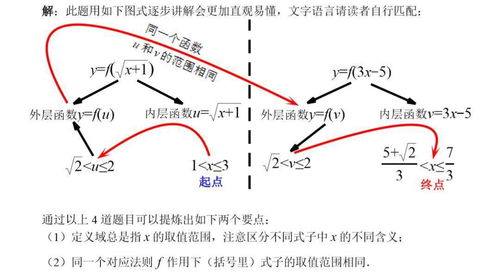
函数f(x),f(g(x)),f(h(x))等函数或复合函数,只要前面对应法则f相同,则定义域的求法为:对应法则f后面括号内的表达式的取值范围相同,即可求出x的范围,即为定义。
复合函数的定义域是怎么规定的?
复合函数的定义域由内层函数和外层函数共同确定的。
例:已知函数y=f(x)的定义域为[0、1],求函数y=f(x2+1)的定义域。
解:∵函数f(x2+1)中的x2+1相当于f(x)中的x(即u=x2+1,与u=x)∴0≤x2+1≤1 ∴。
复合函数定义域
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。
一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不。
